Εξήγηση της γλώσσας MathML

Η αναπαράσταση των μαθηματικών στο διαδίκτυο σε μια οργανωμένη, αναγνώσιμη από προγράμματα πλοήγησης μορφή γίνεται δυνατή από το MathML, ένα πρότυπο που εμπιστεύονται πολλές εκπαιδευτικές και επιστημονικές πλατφόρμες επειδή διατηρεί τους τύπους συνεπείς και αξιόπιστους. Σε αυτό το άρθρο, θα μάθετε γιατί είναι τόσο διαδεδομένο και γιατί έχει σημασία.

Τι είναι το MathML;

Το MathML επιτρέπει στα μαθηματικά να υπάρχουν στον ιστό ως δομημένες πληροφορίες και όχι ως στατικές εικόνες. Αντί να εμφανίζει απλώς τύπους, κωδικοποιεί την εσωτερική τους λογική έτσι ώστε κάθε σύμβολο, τελεστής και σχέση να ορίζεται ρητά και να είναι αναγνώσιμο από μηχανή. Αυτός είναι ο λόγος για τον οποίο το MathML είναι μια βασική τεχνολογία στην επιστημονική δημοσίευση, στις ακαδημαϊκές πλατφόρμες και στους σύγχρονους επεξεργαστές εγγράφων.

Αντί να αποθηκεύει εξισώσεις ως εικόνες, το MathML αναπαριστά τον ρόλο κάθε στοιχείου μέσα σε μια παράσταση. Ένα κλάσμα κωδικοποιείται ως μια δομή αριθμητή-παρονομαστή, μια ρίζα ως μια μαθηματική πράξη, και οι μεταβλητές, οι σταθερές και οι τελεστές αναγνωρίζονται όλοι ξεκάθαρα. Αυτό καθιστά τους τύπους κατανοητούς όχι μόνο στους ανθρώπους, αλλά και στα προγράμματα πλοήγησης, στις μηχανές αναζήτησης, στους αναγνώστες οθόνης και στα υπολογιστικά συστήματα.

Τα θεμέλια XML

Το MathML είναι χτισμένο πάνω σε XML, που σημαίνει ότι οι τύποι γράφονται χρησιμοποιώντας ένθετες ετικέτες. Αυτός ο σχεδιασμός αντανακλά την ιεραρχική δομή των ίδιων των μαθηματικών, όπου οι παραστάσεις αποτελούνται από μικρότερες λογικές μονάδες. Χάρη σε αυτή τη δομή, τα λογισμικά μπορούν αξιόπιστα να εμφανίσουν, να αναλύσουν, να μετατρέψουν και να επεξεργαστούν μαθηματικές εκφράσεις χωρίς ασάφεια.

Δύο συμπληρωματικές διαστάσεις: Παρουσίαση και περιεχόμενο

Το MathML δεν είναι μια μοναδική «γλώσσα» αλλά ένα διπλό-επίπεδο σύστημα:

Παρουσίαση MathML (Presentation MathML)

Ελέγχει λεπτομέρειες διάταξης όπως οι γραμμές κλασμάτων, οι εκθέτες, οι ρίζες, οι αποστάσεις και η στοίχιση, επιτρέποντας στα προγράμματα πλοήγησης να αποδίδουν τις εκφράσεις σωστά στην οθόνη.

Δεν ενδιαφέρεται για το τι σημαίνει το μαθηματικό, αλλά μόνο για το πώς θα πρέπει να εμφανίζεται.

Περιεχόμενο MathML (Content MathML)

Αυτό το επίπεδο κωδικοποιεί μαθηματική σημασία. Αντί να λέει «βάλε αυτό πάνω από εκείνο», λέει «αυτό είναι μια συνάρτηση», «αυτό είναι ένας τελεστής», «αυτό είναι μια εφαρμογή», «αυτό είναι μια σχέση».

Το Content MathML αφήνει τις μηχανές να «σκεφτούν» τον τύπο. Το Presentation MathML τις αφήνει να τον «σχεδιάσουν».

Τα περισσότερα επαγγελματικά εργαλεία — συμπεριλαμβανομένων πλατφορμών που χρησιμοποιούνται στην ακαδημία και σύγχρονων επεξεργαστών — συνδυάζουν και τα δύο επίπεδα για να διατηρήσουν τόσο το νόημα όσο και την εμφάνιση.

Πώς χτίζεται εσωτερικά ένας τύπος

Θεωρήστε μια απλή έκφραση όπως (x² + 1). Στο MathML, αυτή γίνεται ένα δομημένο δέντρο που κάνει την υποκείμενη λογική σαφή:

<code><math>
  <mrow>
    <msup>
      <mi>x</mi>
      <mn>2</mn>
    </msup>
    <mo>+</mo>
    <mn>1</mn>
  </mrow>
</math></code>

Κάθε ετικέτα είναι εξαιρετικά συγκεκριμένη:

• <mi> — αναγνωριστικά (μεταβλητές, σταθερές)
• <mn> — αριθμητικές τιμές
• <mo> — τελεστές
• <msup> — δομές εκθέτη
• <mrow> — ένας περιέκτης ομαδοποίησης

Ακόμη και μια απλή έκφραση γίνεται ένα δομημένο δέντρο. Πιο σύνθετες εκφράσεις — ολοκληρώματα, πίνακες, ένθετες ρίζες — ακολουθούν το ίδιο αναδρομικό μοτίβο. Αυτή η συνέπεια είναι ακριβώς αυτό που επιτρέπει την υψηλής ποιότητας απόδοση και επεξεργασία από μηχανή.

Το MathML σε προγράμματα πλοήγησης, προσβασιμότητα και τον σημερινό ιστό

Τα σύγχρονα προγράμματα πλοήγησης υλοποιούν το MathML εγγενώς, με μηχανές διάταξης που ερμηνεύουν ετικέτες, μετρούν γλυφά, ρυθμίζουν αποστάσεις, ευθυγραμμίζουν γραμμές βάσης και ακολουθούν δεκαετίες κανόνων μαθηματικής στοιχειοθεσίας. Αυτό επιτρέπει στις εκφράσεις MathML να κλιμακώνονται φυσικά με τη σελίδα, να προσαρμόζονται σε διαφορετικά μεγέθη οθόνης, να διατηρούν τυπογραφική συνέπεια, να ενσωματώνονται με CSS και να παραμένουν επιλέξιμες και προσβάσιμες — κάνοντας τα μαθηματικά πραγματικό μέρος του περιεχομένου του ιστού.

Η προσβασιμότητα είναι ένα μεγάλο πλεονέκτημα: οι αναγνώστες οθόνης μπορούν να ερμηνεύσουν τύπους ως λογικές ακολουθίες και όχι ως μυστηριώδεις εικόνες. Οι τεχνολογίες υποβοήθησης μπορούν να πλοηγηθούν μέσα σε μια εξίσωση, να την περιγράψουν προφορικά, να επισημάνουν κάθε στοιχείο βήμα προς βήμα και να απλοποιήσουν σύνθετες σημειογραφίες για χρήστες που χρειάζονται εναλλακτικές αναπαραστάσεις.

Το MathML στο ONLYOFFICE

Τα ONLYOFFICE Docs υποστηρίζουν το MathML. Οι τύποι που επικολλούνται σε μορφή MathML μετατρέπονται αυτόματα στο εσωτερικό μοντέλο εξισώσεων του ONLYOFFICE για σωστή απόδοση και επεξεργασία, διατηρώντας παράλληλα τη δομή και το νόημά τους. Αυτό καθιστά εύκολη την εισαγωγή και επεξεργασία περιεχομένου MathML απευθείας σε έγγραφα, υπολογιστικά φύλλα και παρουσιάσεις.

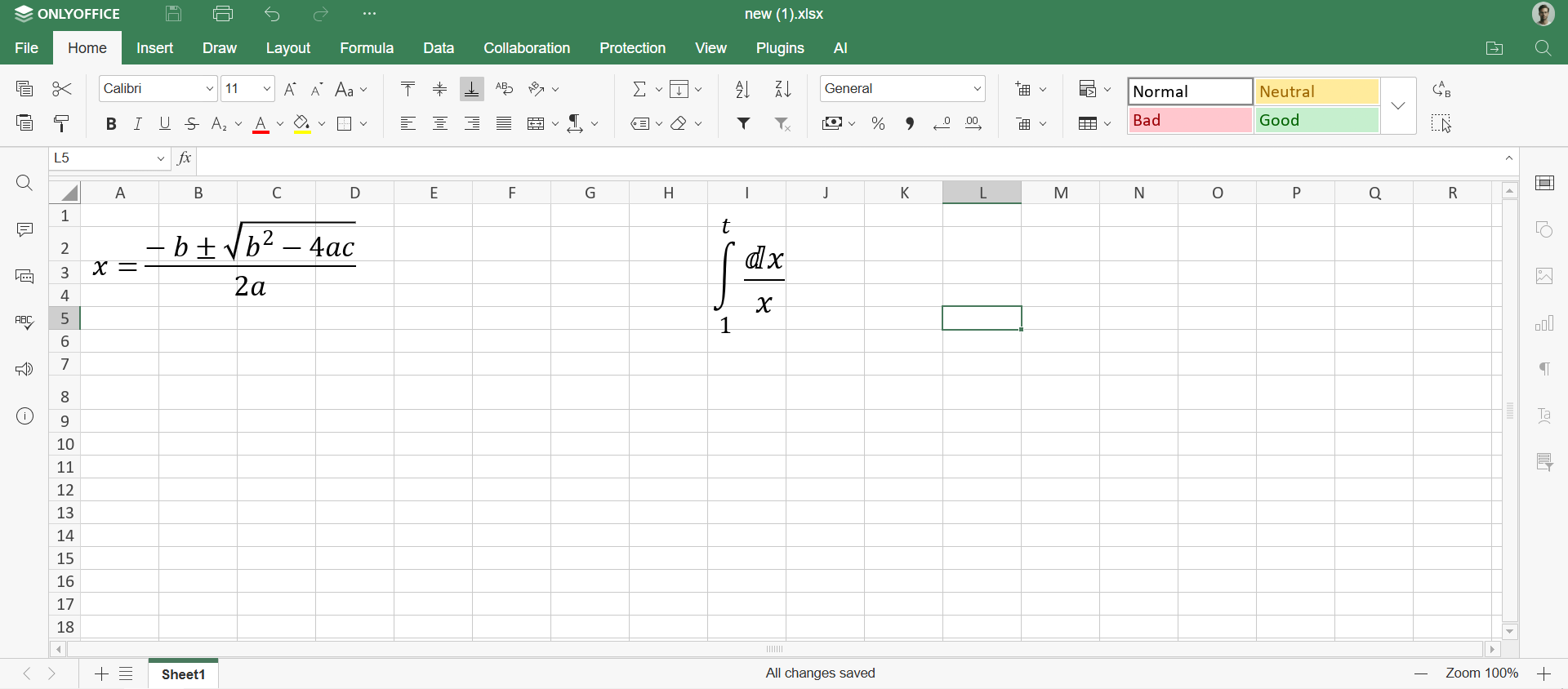
Μόλις προστεθούν, οι τύποι μπορούν να επεξεργαστούν. Απλώς κάντε κλικ στη γραμμή εργαλείων που θα εμφανιστεί αυτόματα μετά την επικόλληση του τύπου.

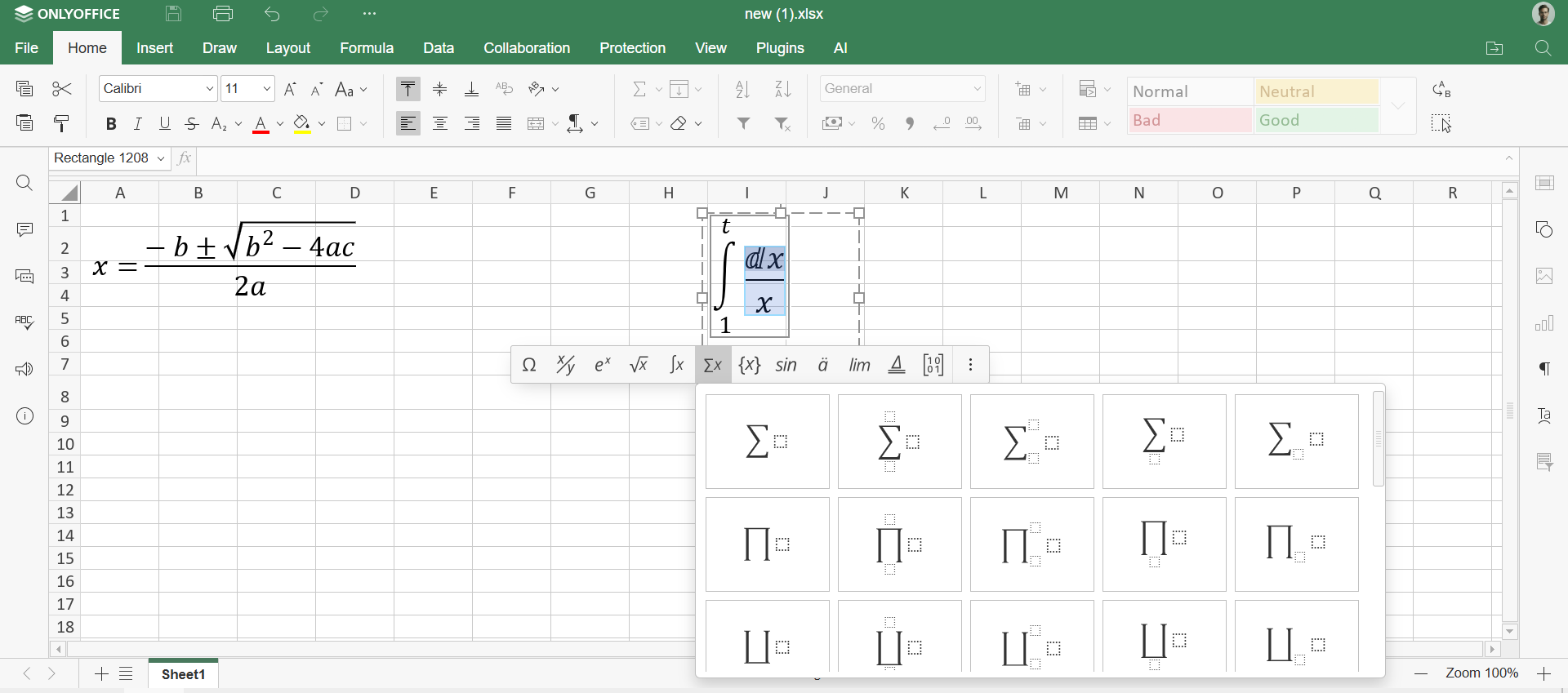
Εάν η γραμμή εργαλείων δεν εμφανιστεί αμέσως, κάντε δεξί κλικ στον τύπο -> Ρυθμίσεις εξίσωσης -> Εμφάνιση γραμμής εργαλείων εξίσωσης

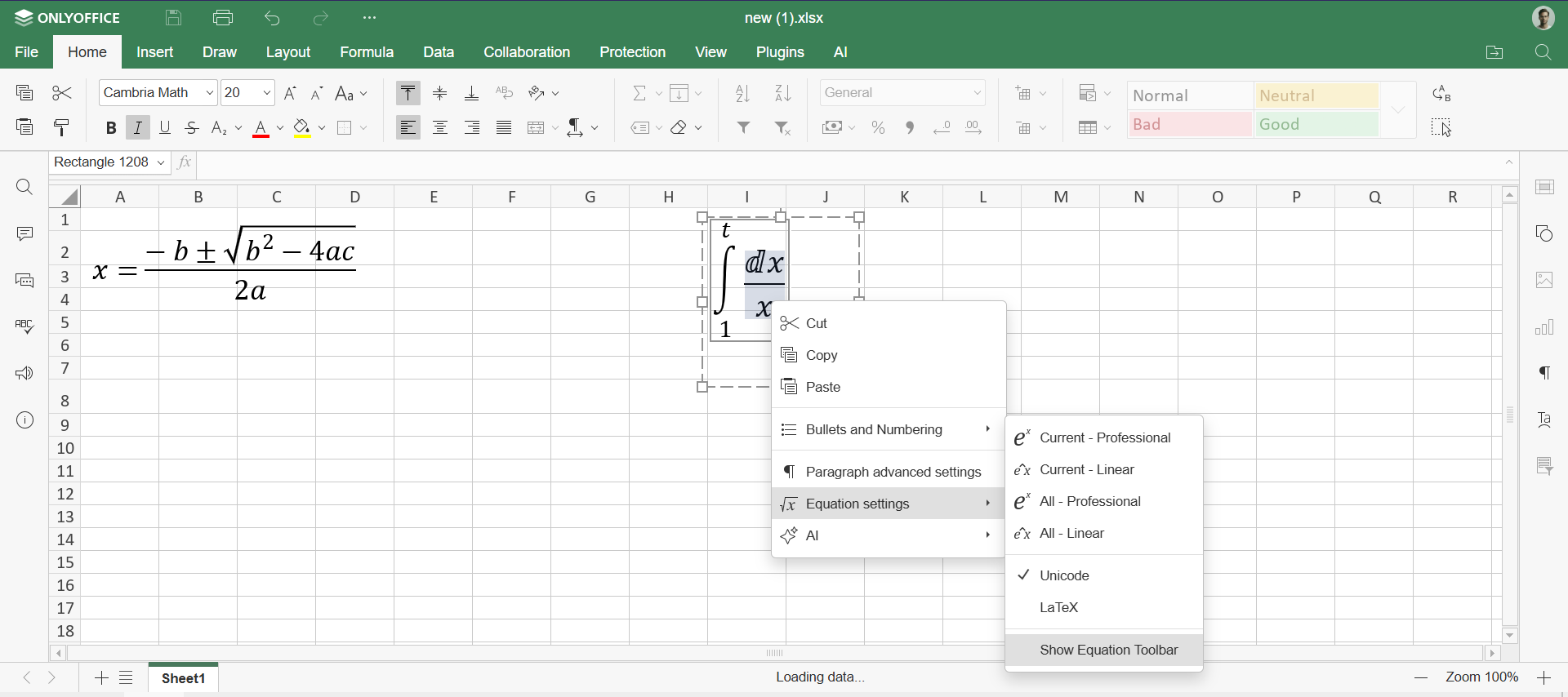
Τώρα μπορείτε να επεξεργαστείτε, να αντιγράψετε και να εισάγετε τον τύπο σε άλλα έγγραφα.

Ξεκινήστε να χρησιμοποιείτε το ONLYOFFICE και κάντε τους τύπους MathML μέρος των εγγράφων σας

Το ONLYOFFICE παρέχει ένα ενοποιημένο περιβάλλον για εργασία με έγγραφα, υπολογιστικά φύλλα, παρουσιάσεις, φόρμες και PDF, με υποστήριξη μαθηματικού περιεχομένου όπως τύπων MathML.

Μπορείτε να εργαστείτε online στο ONLYOFFICE DocSpace ή να χρησιμοποιήσετε τους ONLYOFFICE Desktop Editors για τοπική επεξεργασία σε Windows, Linux και macOS.

ΕΚΚΙΝΗΣΗ ONLINE    ΛΗΨΗ ΕΦΑΡΜΟΓΗΣ ΥΠΟΛΟΓΙΣΤΗ